Kompresja tekstu

dr inż. Aleksander Smywiński-Pohl

konsultacje: pt. 16:30 - 17:30

Klasyfikacja metod kompresji

długość / słownik	stała-do-zmiennej	zmienna-do-zmiennej
	kodowanie różnicowe	kompresja powtórzeń
stały słownik	kodowanie statystyczne	kompresja składowych
zmienny słownik	sekwencyjne kodowanie statystyczne	algorytm Ziva i Lempela

• dla kompresji można wyróznić dwa morfizmy $g$ oraz $h$:
  • $g$ przeprowadza $a \in \Sigma$ w $b \in B^{*} = \{0,1\}$
  • $h$ przeprowadza $b \in B^{*}$ w $c \in B^{*}$
• długość fragmentu tekstu która jest zamieniana dla metod o stałej długości odpowiada najczęściej długości pojedynczej litery $b$ w kodzie binarnym, wtedy $b \in B^{n}$
• słowa $c$ najczęściej mają zmienną długość, dzięki czemu możemy uzyskać kompresję
• morfizm $h$ posiada morfizm odwrotny $h^{-1}$, dzięki czemu możemy skompresowany tekst odtworzyć bez strat
• dla metod o stałym słowniku, $h$ jest stałe w trakcie całego procesu kompresji
• dla metod o zmiennym słowniku $h$ zmienia się w procesie kompresji, a odpowiadająca jej funkcja $h^{-1}$ jest wyliczana w trakcie dekompresji

Kompresja powtórzeń

• zastępowanie powtarzających się wystąpień litery, np. aaaaaaa
• prosta metoda kompresji, np. wykorzystywana do zastępowania białych znaków
• sekwencja $a^{n}$ zastępowana jest napisem $\&an$, gdzie $\& \notin \Sigma$, a $n$ reprezentowane jest w formie binarnej. Jeśli $n > 255$, to zapis dzieli się na fragmenty takie, żeby $n < 256$

Kodowanie różnicowe

• 1980, 1982, 1981, 1985, 1981, ...
• 1980, +2, -1, +4, -4
• Linie faksu:
  • 0101001 0101010 1001001 1101001 1011101 1000000 - linia n
  • 0101000 0101011 0111001 1100101 1011101 0000000 - linia n + 1
  • 0000001 0000001 1110000 0001100 0000000 1000000 - różnica
  • (7,1), (7,4), (8, 2), (10, 1) - zakodowana różnica
  • dobre, jeśli strona zawiera np. pismo odręczne oraz wiele pustej przestrzeni

Statyczne kodowanie Huffmana

• opiera się na obserwacji, że rozkład liter w tekstach nie jest równomierny
• literom pojawiającym się częściej można przyporządkować krótsze sekwencje bitów
• literom pojawiającym się rzadziej można przyporządkować dłuższe sekwencje bitów
• można też przyjąć rozkład a priori (np. wyliczony dla dużego korpusu tekstów), dzięki czemu unikamy konieczności wyliczania prawdopodobieństw oraz umieszczania słownika w pliku wynikowym

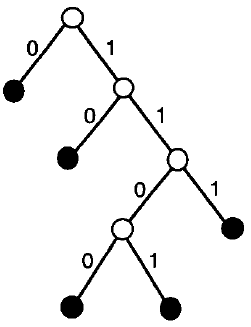
Kod prefiksowy

Żadne słowo $c_i \in B^{*}$ nie jest prefiksem innego słowa $c_j \in B^{*}$, dla $i \neq j$.

Uwaga: każdy kod nie posiadający tej własności, może zostać zastąpiony kodem prefiksowym, bez utraty stopnia kompresji.

Nierówność Krafta - McMillana (3.1)

$\sum_{c_i \in \Gamma} r^{-|c_i|} \leq 1$

1. $\Sigma = \left\{s_1, s_2, s_3, \cdots\right\}$
2. $B^{*} \supset \Gamma = \left\{h(s_1), h(s_2), h(s_3), \cdots\right\} = \left\{c_1, c_2, c_3, \cdots\right\}$
3. $r = |B| = 2$ - rozmiar alfabetu kodów
4. Kraft: isnieje kod prefiksowy $\Leftrightarrow$ spełniona jest nierówność 3.1.
5. McMillan: istnieje jednoznacznie odwracalny kod ze słowami o długościach $l_1, l_2, l_3, \cdots \Leftrightarrow$ spełniona jest nierówność 3.1.

Rozmiar spakowanego tekstu

$|h(text)| = \sum_{a \in \Sigma} n_a \times |h(a)|$

$|h(text)| = \sum_{a \in \Sigma} n_a \times |depth(f_a)|$

gdzie:

• $n_a$ - liczba wystąpień w całym tekście litery $a$
• $depth(f_a)$ - głębokość liścia odpowiadającego literze $a$

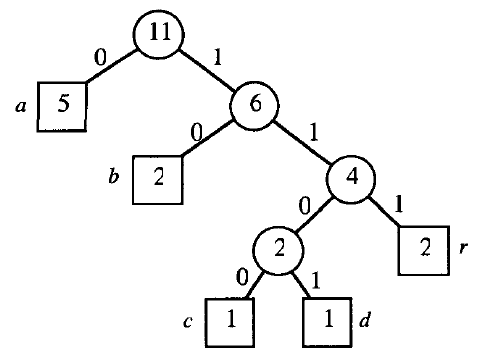
Drzewo Huffmana dla słowa abracadabra

Algorytm budowy drzewa Huffmana

def huffman(letter_counts):
    nodes = []
    for a, weight in letter_counts.items():
        nodes.append(Node(a, weight))
    internal_nodes = []
    leafs = sorted(nodes, key=lambda n: n.weight)
    while(len(leafs) + len(internal_nodes) > 1):
        element_1, element_2 = # elementy nodes i internal nodes o najniższym koszcie, usunięte z list     
        internal_nodes.
            append(Node(element_1, element_2, element_1.weight + element_2.weight)
    return internal_nodes[0]

print(huffman({"a": 5, "b": 2, "c": 1, "d": 1, "r": 2}))

#11 
 0 -> #5 a
 1 -> #6 
  0 -> #2 
   0 -> #1 c
   1 -> #1 d
  1 -> #4 
   0 -> #2 b
   1 -> #2 r

Twierdzenie (3.2)

Algorytm Huffmana tworzy drzewo prefiksów w czasie $O(|\Sigma| log|\Sigma|)$

Dowód: dominującą operacją jest posortowanie liter względem częstości występowania. Pozostałe oparacje mają złożoność liniową ze względu na liczbę liter.

Dynamiczny algorytm budowy drzewa Huffmana

• Wadą zwykłego algorytmu jest fakt, że tekst jest czytany 2 razy
• dynamiczny algorytm czyta tekst tylko raz
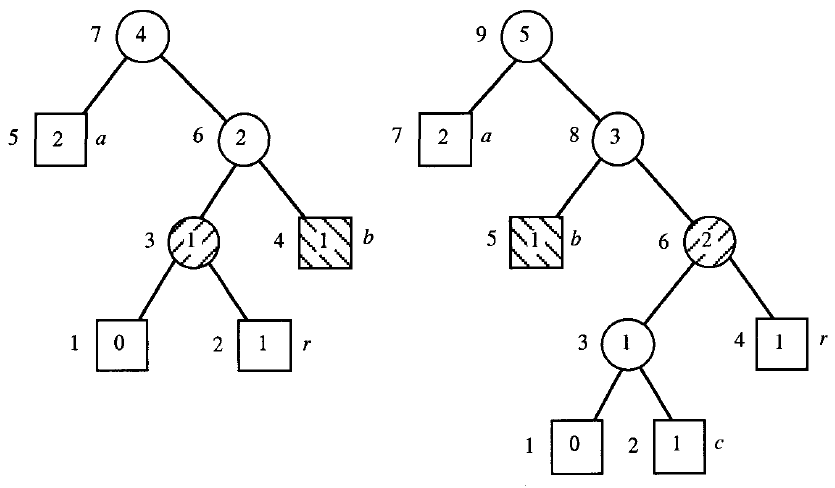
• idea algorytmu polega na budowaniu kolejnych drzew $T_{za}$ na podstawie $T_z$, gdzie $z$ to łańuch znaków, natomiast $a$, to pojedynczy znak
• drzewo budowane jest nad alfabetem $\Sigma \cup \{\#\}$, gdzie $\#$ reprezentuje wszystkie znaki, które nie pojawiły się w fragmencie $z$, wtedy drzewo $T_{z}$ jest drzewem Huffmana, posiadającym następujący koszty:
  • $n_a$ - liczba wystąpień znaku $a$ w $z$
  • $0$ - dla spejcanlego znaku $\#$

from collections import defaultdict

def adaptive_huffman(text):
    Node.nodes = []
    count = defaultdict(int)
    nodes = {"#": Node("#", weight=0)}
    root = nodes["#"]
    for letter in list(text):
        if letter in nodes:
            node = nodes[letter]
            print(node.code() + ' ' + node.letter)
            node.increment()
        else:
            updated_node = nodes["#"]
            print(updated_node.code()  + ' ' + updated_node.letter)
            print("{0:b}".format(ord(letter)) + ' ' + letter)
            node = Node(letter, parent=updated_node)
            nodes[letter] = node
            del nodes["#"]
            zero_node = Node("#", parent=updated_node, weight=0)
            updated_node.add_child(0, zero_node)
            updated_node.add_child(1, node)
            nodes["#"] = zero_node
            updated_node.increment()

adaptive_huffman('abracadabra')

#0(-1,None) #

 #
1100001 a
0 #
1100010 b
00 #
1110010 r
0 a
100 #
1100011 c
0 a
1100 #
1100100 d
0 a
110 b
110 r
0 a

Twierdzenie 3.3 (własność rodzeństwa)

Niech $T$ oznacza kompletne, binarne, wagowane drzewo (z $n$ liśćmi), w których liście mają dodatni koszt, a koszt dowolnego węzła wewnętrznego stanowi koszt jego dzieci. Wtedt $T$ jest drzewem Huffmana wtedy i tylko wtedy, gdy jego liście mogą zostać uporządkowane w następujący sposób:

1. ciąg kosztów $\left(c(x_1), c(x_2), c(c_3), \ldots\right)$ jest niemalejący,
2. $\forall_{1 \leq i < n}: P(x_{2i-1}) = P(x_{2i})$, gdzie $P(x)$ to rodzic $x$.

Problem stanowi dowiedzenie $\leftarrow$, ponieważ $\rightarrow$ wynika wprost z algorytmu Huffmana. Czyli chcemy udowodnić, że mając te dwie własności, dostaniemy drzewo Huffmana.

Dowód jest indukcyjny. Zaczynamy od jakiegoś drzewa $T^i$, w którym mamy węzły $x_1$ oraz $x_2$. Wiadomo, że są to liście, ponieważ koszt jest niemalejący. Liście te mogą być wybrane w kroku algorytmu (choć nie muszą), ponieważ ich koszt jest najniższy. Przyjmijmy, że $x$ to ich rodzic. Rozważmy drzewo $T^{i-1}$, w którym nie ma liści $x_1$ oraz $x_2$. Przyjmując założenie indukcyjne, wywodzimy, że ze spełnienia warunków 1 i 2 drzewo jest drzewem Huffmana. Zatem drzewo $T^{i}$ również jest drzewem Huffmana. Warto zwrócić uwagę, że z własności $T^{i-1}$ wywodzimy własność $T^{i}$, a nie na odwrót.

Kompresja ze zmienną długością bloku

Optymalna kompresja ze zmienną długościa bloku musi uwzględnić 3 zagadnienia:

• znaleźć zbiór podsłów $F$, na który należy podzielić kompresowany tekst $T$,
• znaleźć optymalny sposób podziału tekstu $T$ na podsłowa ze zbioru $F$,
• znaleźć kod $C$, który będzie odpowiadał podsłowom, ze zbioru $F$.

Optymalna kompresja ze zmienną długością bloku jest problemem NP-zupełnym.

Podział tekstu na podsłowa - strategia zachłanna

Dopasuj zawsze najdłuższe słowo występujące w słowniku.

• Jeśli $F$ ogranicza się do liter i podsłów 2-elementowych, to strategia zachłanna jest optymalna.
• Jeśli $F$ zawiera wszystkie swoje pod-słowa, to strategia zachłanna jest optymalna.

Strategia semi-zachłanna

• niech $m = max\{|uv|: u, v \in F \land uv \sqsubset s\}$;
• niech $f_1 \in F$ taki, że $f_1v \sqsubset s \land |f_1v| = m$, dla pewnego $v$;
• wybierz $f_1$ jako kolejny element do zakodowania;
• kontynuuj proces dla $s$ skróconego o $f_1$.

Strategia semi-zachłanna jest optymalna, jeśli $F$ zawiera wszystkie swoje prefiksy.

Algorytm Lempel-Ziv-Welch

from math import ceil
def lempel_ziv_welch(text):
    prefixes = []
    while(len(text) > 0):
        prefix = max_prefix(text, prefixes)
        letter = text[len(prefix)]
        # wypisz indeks prefix-u na ceil(log2(len(prefixes))) bitach
        # wypisz początkowy kod letter na ceil(log(len(alphabet))) bitach
        prefixes.append(prefix + letter)
        text= text[len(prefix)+1:]

Przykład algorytmu, w którym kodowany fragment tekstu ma zmienną długość. W praktyce rozmiar tablicy prefiksów ogranicza się z góry oraz dodaje się do niej wszystkie litery alfabetu.